Fine structure of the hydrogen atom-chemistry learners

Hydrogen fine structure

Introduction to hydrogen fine structure

In our busy mechanical life, maybe you spare some time to enjoy the sunrise or sunset to take the joy of inexplainable moments of natural patterns that feast your eyes. You experience the outreach of sunrays on earth that tune your mind to amicable mood modes. There are a lot of scientific mysteries hidden behind these nature scenarios that we do not know. Yeah, it is true. The sun rays reaching the earth carry spectra of many chemical elements including hydrogen. Today, in this blog article, we will discuss the fine structures of the hydrogen atom.

The standard model of physics explains the basic building blocks of the universe. According to this model, there are four forces that govern the universe. They are electromagnetism, strong force, weak force, and gravitational force. Among them, electromagnetism involves the interaction of the electric and magnetic fields and the light radiations carry it.

Our topic of discussion, the hydrogen fine structure, results from the influence of the intrinsic electromagnetic force of the atom with the photons. It involves the interaction of quantum mechanical spin with the electron's orbital motion.

Fine structure of the hydrogen atom

What is the fine structure of a hydrogen atom?

The splitting of the main spectral line into two or more components with a slight variation in wavelength in the magnetic field is called fine structure in spectroscopy. It means that, in the magnetic field, the electron energy splits to give its sub-states. The electron transitions from these substituent energy levels give additional spectral lines. These are known as fine structures of the main spectral line. The hydrogen spectrum exhibiting the fine structured lines is known as the hydrogen fine spectrum.

Hydrogen is the lightest element with a single electron in the periodic table. The hydrogen atom absorbing external energy shows the excitation of its electron. In a hydrogen atom, the transition of electrons between the two discrete stationary energy levels results in the emission of photons of definite wavelengths. It shows spectral lines in the hydrogen spectrum. Unlike ordinary spectrometers, a high-resolution spectrometer epitomizes the main spectral line splitting into its constituents with a slight variation in their wavelengths. The splitting of spectral emission lines of the hydrogen are known as the hydrogen fine structures.

The scientific explanation image for hydrogen fine structure.

The cleavage of the main spectral line of the hydrogen atom is due to the influence of spin-orbit coupling. The interaction of spin electron magnetic moment with the magnetic field of electron’s relative motion gives the hydrogen fine structures.

Additional reference:

A PowerPoint presentation on the hydrogen fine structure

An infographic explaining the types of the hydrogen spectrum

The hydrogen emission spectrum- PowerPoint presentation

History of the hydrogen fine structure

An atom is the smallest indivisible unit of matter, which forms all the chemical elements that exist in the universe. The protons and neutrons are the fundamental particles of the nucleus, and they bind together to form the central massive positive part of the atom. The electrons are the lightest charged leptons bound to the nucleus with the electrostatic force of attraction to make the atoms.

Since the 1550s, the smelting of ores imparted characteristic colors to the flame. It served as an identification method to find chemical substances in the ores. Since then, spectral studies revealed that the atomic spectrum is a unique characteristic identity for each atom as fingerprints in humans.

The study of the hydrogen spectrum has a remarkable place in astronomy due to its abundance in the universe. Many scientists in the 19th century observed the hydrogen spectral lines while studying the solar spectrum. Similarly, in 1887, Michelson and Morely depicted precisely the absorption trends and spectral emission lines of hydrogen. They demonstrated the small shifts in hydrogen energy levels and the additional spectral emission lines in the hydrogen spectrum. More clearly speaking, they explained the fine structure of the hydrogen atom.

During the 19th century, several atomic theories tried to explain the structure of the atom. But the Bohr model of the atom successfully interpreted the arrangement of electrons around the nucleus.

Additional reference:

What is the history of the hydrogen spectrum?

What is the hydrogen emission spectrum?

Bohr atomic model overview:

Bohr's atomic theory explains the planetary motion of electrons around the nucleus in permitted stationary orbits known as the energy levels. Only those energy levels are allowed that satisfy Bohr's angular momentum condition. And the electron transition between these granted stationary energy levels gives the absorption and the emission spectral lines in the atom.

It gave a groundbreaking theoretical explanation for the spectral emissions of hydrogen by introducing quantized energy shells. It also proved the existence of discrete energy levels with the line spectra of the hydrogen atom. Bohr’s predictions on energy levels of the hydrogen atom closely matched those mentioned by Michelson and Morely. There are a few differences between these two theories. According to Bohr atomic model, a single spectral line ensues in a single electron transition. But according to Michelson and Morely, a single electron transition can give more than one spectral line. Bohr's theory did not explain the exact reason for the spectral line splitting.

In 1913, Neil Bohr put forward this atomic model to explain the electron arrangement patterns for single-electron species like hydrogen. It only demonstrated the coarse structure of the atom. But it failed to explain the atomic structure of multi-electron atoms.

Later, the quantum mechanics predicted that the gross structure of hydrogen line spectra is due to non-relativistic spinless electrons. The Bohr model of the atom explained that the electron without spin orbits the nucleus at lower speeds than the velocity of light. Additionally, the principal quantum number n defines these gross structure energy levels. Hence, it counted one spectral line for every electron transition.

The hydrogen fine structure is the splitting of spectral lines of the hydrogen atom due to the interaction of electron spin with the magnetic field generated by the electron revolution around the atomic nucleus. It is a correction to the non-relativistic Schrodinger equation relativistically. The splitting of spectral lines proved the relativistic and electron spin effects result in the decadence of the energy levels.

In 1916, Arnold Sommerfeld explained the splitting of hydrogen spectral lines with elliptical stationary orbits. And he introduced a dimensionless constant α to account for the energy difference between the gross and fine structure predictions.

Additional reference:

What are the four main postulates of the Bohr atomic model?

An infographic depicting the postulates of the Bohr atomic model?

Spin-orbit coupling

The electrically charged spinning electron acts as a magnetic dipole with equal and opposite magnetic poles in the atom. When the magnetic moment produced by electron spin angular momentum interacts with the magnetic field of the electron's orbital motion is called spin-orbit interaction or spin-orbit coupling.

It is a relativistic interaction of electron spin with orbital angular momentum. It causes the splitting of electron energy levels into their subdivisions with an energy partition equal to the total electron energy. The electron transitions to these sublevels give additional spectral lines due to different transitional energies.

Hence, the spin-orbit coupling is a piece of evidence for the splitting of the main spectral line into two or more ancillary lines. In other words, the interaction of the spin angular momentum of an electron with its orbital angular momentum gives a resultant magnetic field. This effective magnetic field is known as electron spin-orbital angular momentum.

Splitting of hydrogen spectral line

The coupling of the magnetic field generated by the orbiting electron around the nucleus with quantum mechanical spin produces fine structures of the hydrogen spectrum. So, the hydrogen fine structures occur due to the coupling of spin and orbital angular momenta.

Consequently, the total angular momentum quantum number is the sum of spin and orbital angular momentum quantum numbers.

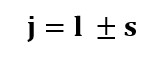The formula for total angular momentum quantum number

Where,

j = total angular momentum quantum number

l = orbital momentum quantum number

s= spin momentum quantum number

The value of l designates the different energy levels of the atom. For example- l=0 we have s-orbit and l=1 we have p-orbit, l=2 we have d-orbit, and so on. The value of j is maximum for parallel spin and orbit momentum quantum numbers.

The neutral particles also show spin-orbit coupling because of the existence of both spin and orbital angular momenta. In semiconductors, the spin-orbit interaction of electrons has huge technical advantages.

Additional reference:

What is angular momentum?

A visual description for the angular momentum of the atom

What is the atomic orbital of an atom?

The electron spin

The electron spin is an intrinsic property of the electron. All the fundamental particles of matter have a spin of 1/2. The spin number defines the number of symmetrical facets an electron can have in one complete rotation to reach the starting point.

We know the path of an electron around the nucleus is circular. So, the electron takes two rotational turns to reach its initial point where it started. Therefore the electron spin is equal to 1/2.

s=1/2

In 1925, Samuel Abraham Goudsmit and George Eugene Uhlenbeck explained the internal spinning motion of the electron. And they interpreted that the electron spin angular momentum is one-half the orbital angular momentum quantum. The two possible spin angular momentum values for the electron are +ħ/2 or –ħ/2.

The quantization of the orientation of angular momentum was confirmed by the German physicists Otto Stern and Walther Gerlach in 1921 with the silver beam experiment.

Additional reference:

What do you know about energy quantization?

An image depicting the energy quantization of the atom

Stern and Walther Gerlach silver beam experiment- evidence for quantized electron angular momentum

The stern-Gerlach experiment demonstrated the quantization of spatial orientation of angular momentum. A beam of neutral silver atoms passed between the poles of a non-uniform magnetic field. And they observed a deflection in the straight path of the electron before they stuck the detector film. To elaborate, half of the silver atoms point toward one direction, and the rest half the silver atoms point in the opposite direction. It implies the silver atoms act as magnetic dipoles in the external magnetic field due to the magnetic field gradient that results in their deflection. In a non-uniform magnetic field, the force exerted on one end of the dipole is greater than the other end dipole force. The net force results from the two opposite magnetic dipoles deflecting the particle’s trajectory.

The Stern-Gerlach experiment

The observations of the detector screen reveal the particle's deflection either up or down by a specific amount. The discrete points of silver atoms accumulate owing to the quantized electron spins.

The silver atom with one unpaired electron in its valence shell spins about its axis. The unpaired silver electron can spin either in the clockwise or anti-clockwise direction. Thus, the electron spin direction creates two possible values as +½ and -½. Consequently, the electron spin creates a small magnetic field that acts like a tiny bar magnet.

The Stern and Gerlach experiment for electrons blends the trajectory in a circle due to Lorentz's force. The electron spin deflects either up or down along the vertical axis with the direction of the magnetic moment. The spin angular momentum values of electrons measured along any axis are +ħ/2 and –ħ/2. They are also known as the intrinsic angular momentum of the spinning electron.

The electron spin orientation

The spinning magnetic dipole of an electron with magnetic moment μ and the magnetic field strength B experiences a torque that rotates it.

Torque of spinning magnetic dipole

An electron with +½ magnetic spin momentum experiences a torque in the magnetic field that rotates it in one direction. Similarly, the electron with -½ magnetic spin momentum experiences a torque that rotates it in the opposite direction. Hence, the potential energy of the magnetic dipole in the magnetic field is the amount of work done in rotating the dipole.

The potential energy of magnetic dipole in the magnetic field

When the magnetic moment vector is parallel to the magnetic field, it is the position of the magnetic dipole aligning itself.

Overview of hydrogen fine structure

As a matter of fact, hydrogen is an alkali metal with a single electron in the 1S-orbit. Let us imagine the absorption of energy transmitting the hydrogen electron from 1S to 2P level. The electron motion is associated with the orbital quantum number (l) and the spin quantum number (s). Hence, the total angular moment quantum number (j) can be expressed as below;

The total angular moment quantum number for the electron

When the electron is in 1S-orbit, its spin quantum number values are +1/2 and -1/2 depending upon the direction of the magnetic moment. And the angular momentum quantum number value for S-orbit is zero. So, the total angular momentum quantum number (j) for the 1S-orbit electron is ±1/2.

The total angular moment quantum number for 1S-orbit electron

Due to the absence of spin-orbit coupling in 1S-orbit, splitting does not take place in electron energy levels. So, the 1S-orbit has a single energy level.

In 2P-orbit, the spin-orbit interaction breaks the main energy level into its components. So, we observe two sub-energy levels for the electron in the 2P-orbit. The spin angular momentum quantum number values for the electron are +1/2 and -1/2. Additionally, the orbital angular momentum quantum number value for P-subshell is 1. The total angular momentum quantum number values are 1/2 and 3/2.

 

The total angular moment quantum number for 2P-orbit

The hydrogen electron transition from 1S-orbit to 2P-orbit gives spectral lines doublet as it involves the two 2P-orbit energy sub-states in the electron transition. The spectral line doublet is a pair of two closely spaced spectral lines with a slight variation in their wavelengths.

The effect of magnetic field on the hydrogen spectral emission lines

The alkali metal atoms with 1S-electron in their valence shell give spectral line doublet in the presence of the magnetic field. But, the alkaline earth metals with two 1S-electrons in their valence shell give spectral line triplet due to spin-orbit interaction. In other words, the number of fine structures increases with an increase in the stable state configurations in the atom. For this reason, Lithium with atomic number three (i.e., n=3) may not be resolved by the average spectroscope. Whereas the Rubidium with atomic number 37 has widely separated spectral emissions and can be observed with a normal spectroscope.

Additional reference:

What are the six series of the hydrogen spectrum?

A visual explanation showing the hydrogen fine structures

 More about the hydrogen fine structures

We know the hydrogen spectrum consists of six spectral series. The names of those six spectral series of hydrogen are;

1. Lyman series
2. Balmer series
3. Paschen series
4. Brackett series
5. Pfund series
6. Humphreys series

An interesting trick to remember all the six series of the hydrogen spectrum easily

The hydrogen atom has a single electron in the 1S-orbit. When the hydrogen atom absorbs energy from the electric current in the discharge tube, it causes the excitation of hydrogen electron from the ground state to the higher energy orbit. After being unstable, the excited electron returns to its initial lower energy state with the emission of photons of suitable wavelengths. When the emitted photons fall on the detector film, it produces the six series of the hydrogen spectrum. In the magnetic field, the spectral lines of hydrogen undergo splitting and create fine structures. Among them, the fine structures of Lyman alpha and hydrogen alpha are most commonly studied based on their significance in astronomy.

An engaging image explaining the series of hydrogen spectrum.

Additional reference:

A PowerPoint presentation on the hydrogen spectral series?

An infographic on the Balmer series of the hydrogen spectrum

Overview of hydrogen spectral emissions

Lyman alpha

Lyman alpha spectral line results in the hydrogen spectrum during the electron transition from the second energy level to the first orbit of the hydrogen atom. It is the most intense spectral emission in the ultraviolet region of the Lyman series that occurs at a wavelength of 121.5 nm. The Lyman alpha spectral line splits to give a pair of spectral lines with a slight variation in their wavelengths due to the spin-orbit interaction.

An infographic explaining the wavelength a wave

As discussed earlier, the transition of an electron from 1S-orbit to 2P-orbit gives a spectral line doublet in the presence of the magnetic field. The Lyman alpha doublet consists of closely spaced two spectral emission lines at wavelengths of about 121.5668 nm and 121.5674 nm. And they are symbolized as Ly-α3/2 and Ly-α1/2 having j values 3/2 and 1/2, where j is the total angular momentum of the electron.

The Lyman alpha doublet picture

The figure shows a longer arrow for j=3/2 during the transition from 1S-orbit to 2P-orbit. It indicates a large energy gap between the two stationary sub-shells for Ly-α3/2 as compared with Ly-α1/2. It realizes Ly-α3/2 is high energy transition than Ly-α1/2. Hence, Ly-α3/2 spectral emission occurs at a slightly shorter wavelength than Ly-α1/2. From this conclusion, we can remind of the quantum theory of radiation for the inversely proportional relationship between the energy of the photon and the wavelengths of emitted light radiation.

Additional reference:

A beautiful infographic on the Lyman series of the hydrogen spectrum?

What is the Lyman alpha line?

What is wavelength?

Hydrogen-alpha

Hydrogen-alpha is the shortest spectral emission in terms of energy in the Balmer series of the hydrogen spectrum. A bright red colored spectral emission at a wavelength of about 656.28 nm in the hydrogen spectrum is nothing but the hydrogen alpha spectral emission. And the hydrogen electron transition from the principal quantum number n=3 to n=2 gives this spectral emission in the visible region of the hydrogen spectrum.

The hydrogen alpha emission line image posted on Apr 1, 2022 on @chemistrylearners Instagram page 

 The magnetic field generated due to the coupling interaction of the spin and the orbital angular momentum of the hydrogen electron during its shift from the 3S-orbit to the 2P-orbit causes the hydrogen-alpha spectral line splitting. The 2P-orbit splits by the magnetic field into the sub-energy states doublet with slightly varying energies. Hence, the electron transition to these modified sub-energy states gives two closely spaced spectral emission lines with a slight difference in their wavelengths.

The hydrogen alpha spectral line splitting

According to Bohr’s energy equation, the energy difference between the second and third orbits of the hydrogen atom is equal to 7.5 eV. The hydrogen-alpha spectral line in the absence of a magnetic field occurs at a wavelength of 656.2 nm. In the magnetic field, the H-α line undergoes splitting into two closely spaced spectral emission lines with a wavelength variation of about 0.016 nm.

The formula calculates the energy difference in the hydrogen alpha spectral emission

Since the start of the spin-orbit coupling interaction concept, we have constantly discussed the splitting of spectral lines by the electron transitions between the S and P-orbits of the atom. So, you might get a question like the one below;

Additional reference:

An infographic explaining the hydrogen alpha spectral line

What is the Balmer series of hydrogen spectrum-a PowerPoint presentation 

An infographic on the comparative explanation of the Balmer series

An exclusive blog post for the Balmer series of the hydrogen spectrum

Did the electron transition only between S and P orbits give spectral splitting?

It is absurd. The atomic structure is not limited to S and P sub-shells. With the increase in atomic number, the number of stationary orbits for the atom increases that it may even include d and f sub-shells. The stationary orbits with non-zero angular momentum quantum numbers give magnetic interaction by the spin-orbit coupling. Let us have a look at the value of l for different sub-shells like s, p, d, and f at once.

The value of l for S-orbit is zero. So, it cannot split into its constituent sub-states. S-orbit has a single energy level irrespective of the value of the principal quantum number. And the l value for p,d,f sub-shells are 1,2,3 respectively. Hence, all these three sub-levels participate in splitting. The electron transition from the S-orbit to any of the three sub-states gives spectral line splitting regardless of the n value.

So, the spectral line splitting is not limited to S and P orbits.

Additional reference:

Why doesthe Balmer series of the hydrogen spectrum occur in two regions, namely ultraviolet and visible but all the other hydrogen spectral series occur in a single zone of the electromagnetic spectrum?

Why the Balmer series is visible?

The visual representation of the hydrogen alpha emission line 

The differences between the Lyman alpha and hydrogen alpha fine structures 

So far, we have discussed the Lyman alpha and hydrogen alpha splitting patterns. Now let us discuss the difference between them.

• The Lyman alpha splitting takes place during the electron transition between the second and first stationary orbits of the hydrogen atom. Similarly, the hydrogen alpha spectral splitting occurs by the electron transition between the third and second stationary orbits.
• The Lyman alpha spectral emission splitting happens by 1S-orbit and 2P-orbit interaction in the magnetic field. But, the hydrogen alpha splitting involves the 3S and 2P orbits spin and angular momentum quantum numbers interaction.
• The energy difference between the two energy levels for Lyman alpha splitting is 10.2 eV. Whereas for hydrogen alpha splitting, the ΔE value is 7.5 eV.
• The Lyman alpha spectral line occurs in the ultraviolet region of the hydrogen spectrum with a wavelength of 121.5 nm. In the same way, the hydrogen alpha spectral line comes in the visible zone of the hydrogen spectrum with a wavelength of about 656.2 nm.
• The wavelength difference for the fines structures of Lyman alpha is 0.0006 nm. And in the case of hydrogen-alpha, it is about 0.016 nm.

Apart from the differences, they both have the most common applications in astronomy. They used to identify quasars, unknown astronomical bodies in the universe. They are also helpful in calculating redshifts.

 The difference between the fine structures of Lyman alpha and hydrogen alpha

Additional reference:

An infographic explanation for the differences between the Lyman alpha and the hydrogen alpha for better understanding

Lorentz force

The Dutch physicist Hendrik Antoon Lorentz was born in Arnhem, Neth, on July 18, 1853. He shared Nobel Prize with Pieter Zeeman in 1902 for the electromagnetic theory of light radiations.

Lorentz interpreted the relationship between electricity, magnetism, and light with his theory. And it was the refined explication of James C. Maxwell's electromagnetic theory.

Maxwell found that the oscillations of electric charges produce electromagnetic radiation. But, he did not clarify the particular charged particle that generated the light radiation.

Later, Lorentz expanded Maxwell's findings to atoms. And he clarified that since the electric current is composed of charged particles, the oscillations of these charged particles are accurately the electron oscillations. And he assumed that these electron oscillations are responsible for the emission of light radiations in the atom.

He added that the electron oscillation was affected by the subsisting magnetic field of the atom that in turn influences the wavelength of emitted light radiation.

Lorentz's investigations were unsuccessful in overcoming the drawbacks of the Michelson-Morely experiment. Therefore, he introduced the local time theory to explain the different time rates of the various locations. He suggested that moving bodies contract their direction of motion while approaching the velocity of light.

The two parametrized vectors, E for the electric field and B for the magnetic field, defined the electromagnetic force acting on a point charge q in the functional form that moves with a velocity v at a given point and time.

And the electromagnetic force is a function of the charge q and its velocity v.

Lorentz force formula

In fact, the test charge q would generate its own finite electric and magnetic fields that alter its electromagnetic force.

If the charge experiences acceleration, it loses its kinetic energy by emitting light radiation. And the emitted light is forced into a curved trajectory.

Trajectory of a particle under magnetic field

Zeeman Effect

The Dutch physicist Pieter Zeeman was born in Zonnemaire, Neth, on May 25, 1865. Zeeman completed his studies at the University of Leiden. And he rendered his service as a physics lecturer at Leiden in 1890. In 1900, Zeeman became a physics professor at the University of Amsterdam. And in 1908, he became the director of the Physical Institute, where he served till his death.

As mentioned earlier, he shared Nobel Prize for physics with Lorentz in 1902 for his discovery of the Zeeman Effect.

Zeeman elucidated the effect of a magnetic field on a source of light. He explained the cause for the splitting of emitted light radiations of the atomic spectra.

The interaction of the light source of the atom with the external magnetic field to split the spectral lines into their fine structures was named the Zeeman Effect. While experimenting on the yellow D-lines of sodium, Zeeman first observed it in 1896.

When the sodium emission lines passed through the external magnetic field, the broadening of the sodium spectral line took place. And it showed the splitting of distinct spectral lines into 15 components.

From the experimental evidence, he concluded that the electron movement from one discrete energy level to the other causes the emissions of photons of definite wavelengths, which give spectral lines in the atomic spectra. A quantity named angular momentum characterizes each distinct energy level of the atom. In the absence of a magnetic field, there is no splitting in the atomic energy levels. Hence, they exhibit a single spectral line even under a high-resolution spectrometer.

But in the external magnetic field, these stationary energy levels of atoms split into their sub-states of slightly different energies. The electron transitions to these sub-states of energy give more spectral lines than expected. In other terms, it is referred to as the splitting of the main spectral line into its components in the external magnetic field. The additional spectral lines are also known as fine structures. The phenomenon is known as the Zeeman effect.

Applications of Zeeman effect

We all know the splitting of spectral lines served as an efficient method to identify the magnetic field strength in the chemical elements. In addition to this, the Zeeman effect helped in the following ways.

The Zeeman effect helped scientists specify the atomic energy levels in terms of angular momenta.

It presented an effective method to study the atomic properties concerning atomic nuclei like electron paramagnetic resonance.

It calculated the magnetic effects of spectral lines effectively. Therefore, it is used to estimate the magnetic fields of celestial bodies in astronomy.

Overview of the Zeeman effect

Zeeman suggested a mathematical formula to calculate the number of fine structures in spectral line splitting by the external magnetic field.

Zeeman formula

Where,

L is the orbital angular momentum quantum number and its value can be a non-negative integer.

The following table describes the value of the orbital angular momentum quantum number for various atomic levels.

Table for calculation of number of spectral lines by the Zeeman formula

The above table explains the number of spectral lines obtained by the interaction of the external magnetic field with the light source. And the number of hydrogen fine structures due to the interference of the external magnetic field in the hydrogen electron transition from S-orbit to P-orbit is three.

 The S-orbit has zero orbital angular momentum number. And it does not show spectral line splitting even in the external magnetic field. Hence, it has a single energy level.

But, for P-orbit, the value of l=1. Consequently, in an external magnetic field, it splits into three sub-energy states that give three hydrogen fine structures by the spectral line splitting.

The Zeeman effect splitting pattern

Regardless of the principal quantum number value, the hydrogen electron transition involves the similar S and P atomic sub-levels in the Lyman alpha or hydrogen-alpha. Hence, the previous explanation justifies these spectral emissions.

The spectral lines which show the Zeeman Effect exhibits polarization. This phenomenon affects the direction of the vibrating electromagnetic field. It influences the appearance of the spectral emission lines.

A sunspot emits three spectral lines by the influence of a strong magnetic field due to the Zeeman effect. Only two among the three spectral lines are visible from the top view due to the polarization effect. The suppression in the spectral line visibility gets over by changing the observer's direction of view. With the change of angle of observation, a weak third spectral line appears.

Why is the difference in the number of fine structures observed for the spin-orbit coupling and Zeeman effect?

 The concept behind the two mentioned phenomena is the same. The hydrogen electron, while absorbing energy, undergoes a transition between the discrete transition states, and the process goes on with the emission of photons of varying frequencies that result in spectral lines in the spectrum.

The interference of the magnetic field with the light source causes spectral line splitting that gives rise to fine structures.

In spin-orbit coupling, the electron spin interacts with the orbital angular momentum. Thus, it creates an internal magnetic field. And the generated magnetic field splits the main spectral line into its fine structures.

Similarly, When passed through the poles of an external magnetic field, the light source shows the spectral line splitting known as the Zeeman effect.

For example- The electron transition from S-orbit to P-orbit gives two spectral lines in the spin-orbit coupling. Besides, the same electron transitions result in three spectral lines by the Zeeman effect. It solely depends on the nature of the magnetic field that interacts with the emitted light. Hence, we observe a difference in the number of spectral lines in both phenomena.

Additional reference:

A beautiful visual interpretation for the Zeeman effect

 Paschen back effect:

This effect is observed when the emitted light source passes through the strong magnetic field. The hydrogen atom on the absorption of energy shows an electron transition that emits photons of definite wavelengths. These emitted light radiations show spectral lines when entrapped on the detector film. The emitted photons that pass through a strong external magnetic field poles show a different pattern of spectral splitting when analyzed by the high-resolution spectrometer. This spectral splitting is due to the coupling of the external magnetic field with the light source. And it is known as the Paschen back effect. Two German physicists, Paschen and Ernst Back in 1921, observed this effect for the first time.

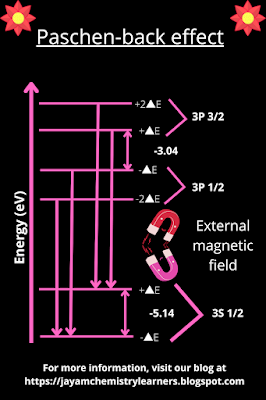The explanation for the electron transitions in the sodium atom by the Paschen back effect

The energy difference is expressed as a multiple of Bohr magneton (μ_B)

The energy difference formula for Paschen back effect

Sodium is used to interpret this model for convenience. The spectral line splitting in the sodium metal depicts that the transition of an electron from 3S-orbit to sub-energy levels of 3P-orbit gives different kinds of spectral emission lines than the Zeeman effect. The resulting spectrum shows a triplet, with the central spectral line having double the intensity as the remaining two spectral emission lines.

The Paschen-back effect conditions are in the sun for Lithium spectra. It does not have much astronomical significance.

Additional reference:

A visual representation for the Paschen back effect for easy understanding

What is the Paschen series of the hydrogen spectrum?

The differences between the Zeeman effect and the Paschen back effect:

So far, we have discussed the effect of the magnetic field on spectral line splitting. We discussed the two kinds of magnetic field interactions. They are external magnetic field and internal magnetic field interactions.

Based on the magnetic strength, the magnetic field is of two types.

• Weak magnetic field
• Strong magnetic field

Case-I: Weak magnetic field (Zeeman effect)

The interaction of spin and orbital angular momentum is stronger than the external magnetic field coupling in the case of the weak magnetic field. In such scenarios, the Spin-orbit effect is a dominant factor that causes spectral line splitting. The coupling of orbital angular momentum quantum number with electron spin angular momentum generates spin-orbit coupling. The induced internal magnetic field splits the spectral line into its components. Hence, the source of light that passes through the poles of the weak magnetic field diverges the spectral emission line due to spin-orbit interaction. The Dutch physicist Pieter Zeeman in the year 1896, observed this splitting on the yellow D-lines of sodium. And it is known as the Zeeman effect.

The demonstration of magnetic field in the Zeeman effect

The amount of splitting is less when compared with the energy difference between the unperturbed levels in the weak magnetic fields.

Both the orbital angular momentum vector and the electron spin vector jointly contribute to the direction of the magnetic field.

The total angular momentum quantum number is the sum of the two vector quantities, i.e., orbital angular momentum quantum number and electron spin quantum number.

Case-II: Strong magnetic field (Paschen back effect)

The presence of the large magnetic field disrupts the interaction of the spin and orbital angular momentum quantum numbers of the atom. The source of light that passes through the poles of a strong magnetic field shows a different splitting pattern due to the interaction with an external magnetic field rather than spin-orbit interaction. The decoupled spin-orbit interaction in the sufficiently large external magnetic field leading to the spectral line splitting with more fine structures is known as Paschen back effect. Two German physicists, Paschen and Ernst Back in 1921, observed this effect for the first time.

The demonstration of magnetic field in the Paschen back effect

The amount of splitting is considerable when compared with the energy difference between the unperturbed levels.

The orbital angular momentum vector and the electron spin vector individually define the direction of the magnetic field.

The total angular momentum quantum number is no longer a constant for particle motion.

 Additional reference:

An infographic on the differences between the Zeeman effect and the Paschen back effect

Question and answers on the hydrogen fine structure topic:

Why did Bohr's atomic model fail to explain the fine structures of the hydrogen atom?

Bohr atomic model successfully explained the electronic arrangement of the atom with quantized electron orbits. Still, it could not explain the thin and narrow splitting structures of the hydrogen spectrum. The following reasons might be an accurate explanation for this limitation.

1. Non-relativistic spin less electron motion could not produce a magnetic field in the atom.
2. The Bohr model of the atom explained that the electron without spin orbits the nucleus at lower speeds than the velocity of light.
3. Additionally, the principal quantum number n defines these gross structure energy levels. Hence, it counted one spectral line for every electron transition.

All these misinterpretations result in the gross spectral structures in the hydrogen spectrum.

For an interesting infographic on Bohr model Vs. fine structures of hydrogen atom, refer here.

Why does the splitting structures of the atom named fine structures?

The spectrum observations with an ordinary spectrometer cannot reveal the thin, narrow, delicate structures of a spectral line resulting from the electron transition. But a high refined spectrometer can divulge them. The single spectral line of an atomic spectrum is a collection of silky-splitting structures when hit by a magnetic or electric field. These unequal energy lines were named fine structures based on their appearance after the invention of high refined spectrometers.

Did the atomic number affect the splitting of spectral lines?

Yes, the number of fine structures increases with an increase in the stable state configurations in the atom.

The alkali metal atoms with one 1S-electron in their valence shell give spectral line doublet in the presence of the magnetic field. But, the alkaline earth metals with two 1S-electrons in their valence shell give spectral line triplet due to spin-orbit interaction. 

An average spectrometer cannot show the fine structure of the Lithium under ordinary conditions. But, the same spectroscopic observation circumstances can divulge the widely spread spectral emissions of Rubidium metal due to its high atomic number and consequently more stable state configurations.

Who explained the fine structures of the hydrogen spectrum with relativistic corrections?

Arnold Sommerfeld, the German physicist who pioneered the atomic and quantum physics evolutions and guided many chemistry and physics Nobel Prize winners to achieve their scientific goals, had explained the fine structures of the hydrogen spectrum with relativistic corrections.

Neil Bohr's model of atom explicated the line spectrum of hydrogen with non-relativistic electron motions. But, these assumptions failed in interpreting the fine spectral structures.

Sommerfeld recognized this opportunity to add relativistic corrections to hydrogen spectral emissions. And his fine structure constant α elucidated the gap between the gross Bohr spectral structures and the fine structures of spectral splitting.

Fine structure constant representation

To point out the unequal energy distributions of spectral splitting, he introduced the second quantum number (azimuthal quantum number) to explain the orbital angular momentum of the electron.

The azimuthal quantum number invention and relativistic electron motion corrections solved the fine structure limitation.

Conclusion:

We hope that this blog post is helpful to you. And what else do you know about the fine structures of the hydrogen atom? Kindly share your knowledge with us in the comments below. And also, you can visit our blog https://jayamchemistrylearners.blogspot.com/ regularly for more engaging topics of chemistry. We add new posts regularly to our blog. To not miss any updates, kindly follow us. We will notify you immediately. Most importantly, you can ask your questions on the hydrogen fine structures  topic in the post comment section and also on our Instagram page. We are happy to hear from you and will answer you.

For more fascinating chemistry topic visuals, please visit and follow our Instagram page @chemistrylearners and Pinterest page @kameswariservices.